Продолжаем описывать популярные алгоритмы из data mining, сегодня остановимся на методе к-средних (k-means).
Метод к-средних создает к-групп из набора объектов таким образом, чтобы члены группы были наиболее однородными. Это популярная техника кластерного анализа для исследования набора данных.
А что такое кластерный анализ? Кластерный анализ – это семейство алгоритмов, разработанных для формирования групп таким образом, чтобы члены группы были наиболее похожими друг на друга и не похожими на элементы, не выходящие в группу. Кластер и группа – это синонимы в мире кластерного анализа.
Есть какой-нибудь пример? Определенно. Предположим, что у нас есть данные о пациентах. В кластерном анализе это называется наблюдениями. Мы кое-что знаем о каждом пациенте, например, его возраст, пульс, кровяное давление, максимальное потребление кислорода, холестерин и так далее. Это вектор, представляющий пациента.
Смотрите:
Вы можете думать об этом векторе как о списке чисел, который может быть интерпретирован в виде координатов многомерного пространства. Пульс в одном измерении, кровяное давление – в другом и так далее.
Может возникнуть вопрос:
Как нам сгруппировать вместе пациентов по возрасту, пульсу, давлению с помощью этих векторов?
Хотите узнать хорошую новость?
Вы говорите методу к-средних, сколько кластеров вам нужно, а он сделает все остальное.
Как это происходит? Метод к-средних имеет множество вариантов работы для различных типов данных.
В общем случае все они делают примерно следующее:
- Метод к-средних выбирает точки многомерного пространства, которые будут представлять к-кластеры. Эти точки называются центрами тяжести.
- Каждый пациент будет располагаться наиболее близко к одной из точек. Надеемся, что не все они будут стремиться к одному центру тяжести, поэтому образуется несколько кластеров.
- Теперь у нас есть к-кластеров, и каждый пациент – это член какого-то из них.
- Метод к-средних, учитывая положение членов кластера, находит центр каждого из к-кластеров (именно здесь используются векторы пациентов!).
- Вычисленный центр становится новым центром тяжести кластера.
- Поскольку центр тяжести переместился, пациенты могли оказаться ближе к другим центрам тяжести. Другими словами, они могли сменить членство.
- Шаги 2-6 повторяются до тех пор, пока центр тяжести не перестанут изменяться и членство не стабилизируется. Это называется сходимостью.

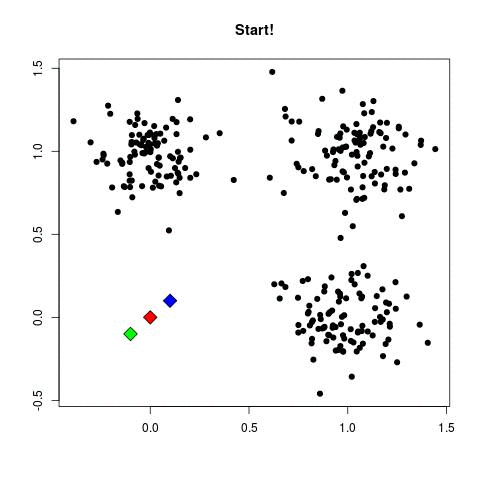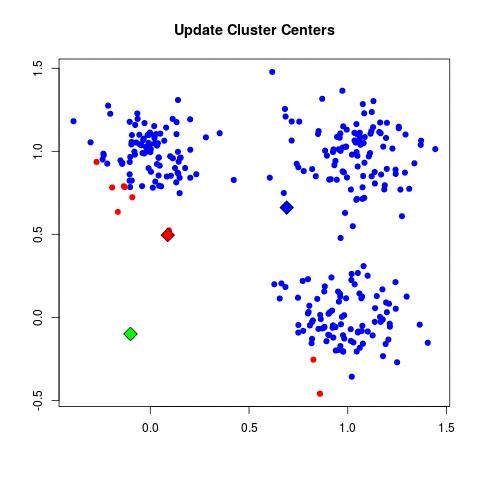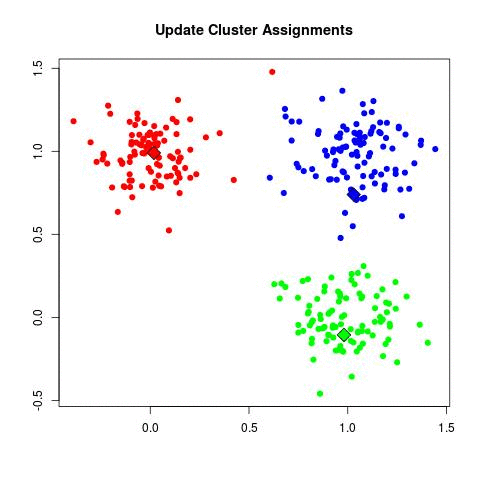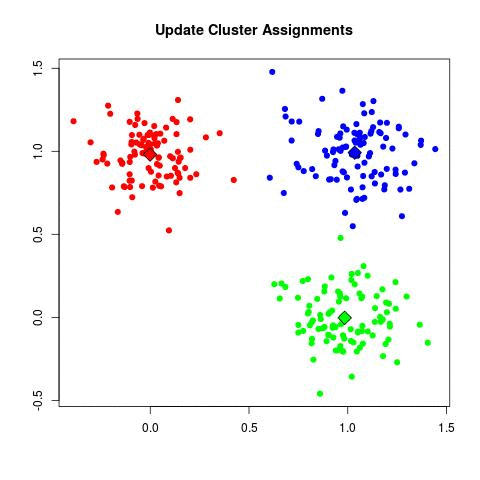
Требует ли этот метод обучения или он самообучающийся? Бывает по-разному. Но большинство расценивает метод к-средних как самообучающийся. Вместо того, чтобы уточнять количество кластеров, метод к-средних «изучает» кластеры самостоятельно, не требуя информации о том, к какому кластеру относятся данные наблюдения. Метод к-средних может быть полуобучаемым.
Почему стоит использовать метод к-средних? Не думаю, что многие возьмутся спорить:
Основным достоинством алгоритма является его простота. Простота обычно означает высокую скорость выполнения и эффективность по сравнению с другими алгоритмами, в особенности при работе с крупными наборами данных.
Дальше – лучше:
Метод к-средних может использоваться для предварительного разбиения на группы большого набора данных, после которого проводится более мощный кластерный анализ подкластеров. Метод к-средних может использоваться, чтобы «прикинуть» количество кластеров и проверить наличие неучтенных данных и связей в наборах.
Но не все так гладко:
Два основных недостатка метода к-средних заключаются в чувствительности к «выбросам» и начальному выбору центров тяжести. Также нужно помнить, что метод к-средних создан для работы с непрерывными значениями, поэтому придется проделать пару фокусов, чтобы заставить алгоритм работать с дискретными данными.
Где он используется? Огромное количество реализаций метода к-средних доступны онлайн:
Видео метода к-средних
Метод к-средних в R
|
1 2 3 4 5 |
kmeans(x, centers, iter.max = 10, nstart = 1, algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"), trace=FALSE) ## S3 method for class 'kmeans' fitted(object, method = c("centers", "classes"), ...) |
Arguments
x |
numeric matrix of data, or an object that can be coerced to such a matrix (such as a numeric vector or a data frame with all numeric columns). |
centers |
either the number of clusters, say k, or a set of initial (distinct) cluster centres. If a number, a random set of (distinct) rows in x is chosen as the initial centres. |
iter.max |
the maximum number of iterations allowed. |
nstart |
if centers is a number, how many random sets should be chosen? |
algorithm |
character: may be abbreviated. Note that "Lloyd" and "Forgy" are alternative names for one algorithm. |
object |
an R object of class "kmeans", typically the result ob of ob <- kmeans(..). |
method |
character: may be abbreviated. "centers" causes fitted to return cluster centers (one for each input point) and "classes" causes fitted to return a vector of class assignments. |
trace |
logical or integer number, currently only used in the default method ("Hartigan-Wong"): if positive (or true), tracing information on the progress of the algorithm is produced. Higher values may produce more tracing information. |
Примеры
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
require(graphics) # a 2-dimensional example x <- rbind(matrix(rnorm(100, sd = 0.3), ncol = 2), matrix(rnorm(100, mean = 1, sd = 0.3), ncol = 2)) colnames(x) <- c("x", "y") (cl <- kmeans(x, 2)) plot(x, col = cl$cluster) points(cl$centers, col = 1:2, pch = 8, cex = 2) # sum of squares ss <- function(x) sum(scale(x, scale = FALSE)^2) ## cluster centers "fitted" to each obs.: fitted.x <- fitted(cl); head(fitted.x) resid.x <- x - fitted(cl) ## Equalities : ---------------------------------- cbind(cl[c("betweenss", "tot.withinss", "totss")], # the same two columns c(ss(fitted.x), ss(resid.x), ss(x))) stopifnot(all.equal(cl$ totss, ss(x)), all.equal(cl$ tot.withinss, ss(resid.x)), ## these three are the same: all.equal(cl$ betweenss, ss(fitted.x)), all.equal(cl$ betweenss, cl$totss - cl$tot.withinss), ## and hence also all.equal(ss(x), ss(fitted.x) + ss(resid.x)) ) kmeans(x,1)$withinss # trivial one-cluster, (its W.SS == ss(x)) ## random starts do help here with too many clusters ## (and are often recommended anyway!): (cl <- kmeans(x, 5, nstart = 25)) plot(x, col = cl$cluster) points(cl$centers, col = 1:5, pch = 8) |
Метод к-средних в Python
scipy.cluster.vq.kmeans
- scipy.cluster.vq.kmeans(obs, k_or_guess, iter=20, thresh=1e-05)
| Parameters: |
obs : ndarray
k_or_guess : int or ndarray
iter : int, optional
thresh : float, optional
|
|---|---|
| Returns: |
codebook : ndarray
distortion : float
|
Примеры
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
from numpy import array from scipy.cluster.vq import vq, kmeans, whiten features = array([[ 1.9,2.3], ... [ 1.5,2.5], ... [ 0.8,0.6], ... [ 0.4,1.8], ... [ 0.1,0.1], ... [ 0.2,1.8], ... [ 2.0,0.5], ... [ 0.3,1.5], ... [ 1.0,1.0]]) whitened = whiten(features) book = array((whitened[0],whitened[2])) kmeans(whitened,book) (array([[ 2.3110306 , 2.86287398], [ 0.93218041, 1.24398691]]), 0.85684700941625547) |
|
1 2 3 4 5 6 7 |
from numpy import random random.seed((1000,2000)) codes = 3 kmeans(whitened,codes) (array([[ 2.3110306 , 2.86287398], [ 1.32544402, 0.65607529], [ 0.40782893, 2.02786907]]), 0.5196582527686241) |
Дополнительно взгляните на еще одну реализацию метода в Питоне scipy.cluster.vq.kmeans2
Реализации метода в MathLab и других платформах можно найти по ссылкам выше.
